Theory

Introduction

Zap is a new program for solution of the Poisson-Boltzmann Equation (also referred to as the PBE). This is an approach that allows the calculation of a variety of electrostatic properties for neutral and charged molecules. Electrostatic interactions are very important to many biological processes. To understand the nature of these interactions it is crucial to characterize the physical and chemical properties of these biological molecules in solution, which is their natural state. While the principles of solvent effects on solutes have been known for a long time, the application of these principles to enable predictions of experimentally-observable properties have not been available. Recently, with the advent of structure-based drug design and protein engineering, and the growing interest in de novo predictions of protein folding, the importance of accurately describing the electrostatic environment of biomacromolecules has come to the forefront.

The most accurate model for understanding the properties of aqueous solutions would be to explicitly model all molecules in the system, including the solvent molecules using a molecular mechanics approach. The electrostatically important portions of a typical molecular mechanics force field are the Coulombic and van der Waals terms. Of course this would entail calculations of interactions between each solvent molecule and each "solute" molecule as well as between the solvent molecules themselves. Also significant is that this calculation would have to be performed and averaged for many solvent molecule configurations to account for molecular motion and entropy. While this is possible for some systems on a conventional workstation, and other systems on a supercomputer, it is not particularly practical.

A complementary approach, using the empirical free energy information from LogP_o/w, which implicitly incorporates solvation effects, is provided by the HINT program. HINT is also available from eduSoft LC.

Another alternative is to use continuum or macroscopic methods, which treat solvents not as discrete molecules, but as environmental properties with average values. In particular, the electrostatic properties of solvents such as water can be described with descriptors for charge, dielectric, etc. In this chapter we will discuss the solution of the PBE as implemented in programs such as DelPhi, followed by a description of the enhancements that are incorporated in the Zap algorithms.

The Poisson-Boltzmann Equation (PBE)

In classical electrostatics materials are considered to be homogeneous dielectric media that can be polarized by electrical charges. A dielectric constant can be considered a bulk measure of the polarizability of the media. This is a continuum model because the polarization of each atom is not considered. Coulomb's law, eqn. 1, describes the Electrostatic energy, E_ij in terms of two charges, q_i and q_j, the distance between the atoms, r_ij and the dielectric constant :

(eqn. 1)

The potential, _i at atom i is given by:

(eqn. 2)

For instance, two charges of +1 separated by one Ångstrom in vacuum (, dielectric = 1.0) have an energy of 560.9 kT (where k is Boltzmann's constant and T is temperature in K) or 331 kcal/mol. It is important to note that this model is only valid for an infinite medium of uniform dielectric, which is certainly not the actual case in a complex solution of biomacromolecules, ligands and polar solvent (like water). And of course, these are the types of problems we are most interested in.

Biomacromolecules such as proteins have rather low dielectrics (typically 2-5) because their polar groups and side chains are more or less frozen in place and cannot actually reorient significantly in response to an externally applied dielectric field. Also, many portions of macromolecules are apolar. However, water has a dielectric constant of around 80 and is able to re-orient its dipoles freely. Thus a biomacromolecular system in aqueous solution has two extremely different dielectric properties for the two components, macromolecule and water. The Poisson-Boltzmann Equation (PBE) is capable of modeling this type of situation.

The electrostatic field, F, and electrostatic displacement, D, as functions of r can be written as:

(eqn. 3)

Note that is rigorously a tensor, i.e. the polarization can, in theory, be in a different direction from the polarizing field. In practice this is ignored and it is treated as a scalar quantity. In an inhomogeneous dielectric media with charges, Poisson's equation relates the electric displacement to the charge density (r):

(eqn. 4)

By substituting D(r) from eqn. 3,

(eqn. 5)

It is useful to separate the charge density, (r), into two parts:

(eqn. 6)

where _inside is the charge distributions of all the fixed charges inside the molecule, and _outside is the charge density outside the molecule (i.e., solvent) which accounts for reorientation and redistribution of (ion) charges in the solution.

The charge density, _outside, can be modeled by a Boltzmann distribution. If the charge density of the molecule is low then:

(eqn. 7)

where is the dielectric constant of the solvent, is the electrostatic potential in units of kT/e, e is the charge of an electron, N_A is Avogadro's number, I is the ionic strength in moles/liter, k is Boltzmann's constant, T is temperature in K, and ' is the Debye-Hückel inverse length. Note that ' appears with a negative sign because charge accumulates of opposite sign to the inducing potential.

Substituting eqn. 7 into the Poisson equation (eqn. 5) gives the linear form of the Poisson-Boltzmann equation:

(eqn. 8)

where '₀ is 0 inside the molecule and ' outside the molecule (i.e., in the solvent).

Because it includes the effects of solvent/molecule dielectric as well as ionic strength, the Poisson-Boltzmann equation is a good model for the electrostatic properties of complex biological systems, except that it cannot be solved analytically for any but the simplest dielectric boundary shapes; e.g., spheres, etc. Numerical approximations such as the Finite Difference Algorithm are required to solve the PBE for the complex shapes and structures of biological molecules in solution.

Finite Difference Solution of PBE

The numerical solution usually chosen to solve the PBE is to map the molecule onto a three dimensional grid and apply the finite difference approximation. A two dimensional representation of this is shown below. Note that the grid spacing is shown as d, and that the interior of the molecule is assigned a dielectric _inside different from the exterior of the molecule (solvent) which is assigned a dielectric _outside.

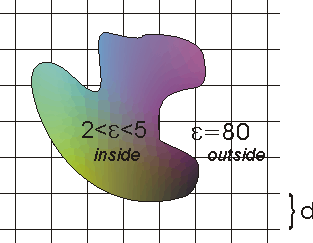
The PBE must be satisfied everywhere in the system, but most importantly at each of the grid points. If a cube of dimension d x d x d is considered to surround each grid point, the derivatives in eqn. 8 can be replaced by "finite differences" measured in the cube. Thus, the functions , and can be represented by their values at grid points.

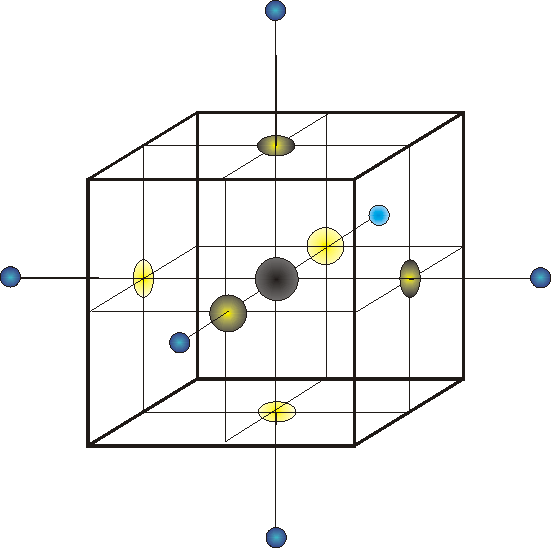
In the figure above, the black sphere represents the grid point of interest (i=0), the blue spheres are the six neighboring grid points (i=1-6). For each of these seven points in space are associated values of q_i (charge), _i and '₀. The yellow spots, on the surface of the cube surrounding grid point 0, identify the dielectric constants, which are calculated half-way between grid point 0 and each of its six neighbors.

The potential at any grid point (0) depends on q₀, '₀ with grid spacing, d, and the potential, _i, and dielectric, _i, of the neighboring six grid points:

(eqn. 9)

where N = 1 for the linear case (eqn. 8) or N = (1 + ₀²/3! + ₀⁴/5! + ...) for the non-linear case if the charge density of the molecule is not low and/or the ionic strength of the solution is not low.

From this the potential at each grid point can be calculated. It is important to note that these potentials will adjust as a function of the potential of the neighboring grid points. Thus, this calculation is iteratively repeated to increase the accuracy and precision of the potentials. A set of convergence criteria must be established for each run.

Electrostatic Potentials

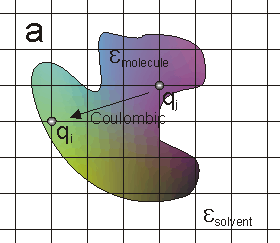
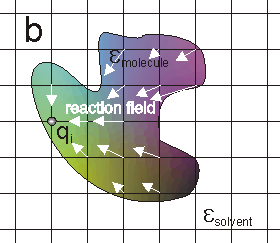
The most basic electrostatic quantity is the electrostatic potential. The potential at a charge can be considered to be comprised of three terms: the Coulombic potential from all the other charges (figure a), the reaction of the solvent to the charge (figure b), the reaction of the solvent to all the other charges (figure c).

(eqn. 10)

The utility of this decomposition is that it represents: The regular vacuum force-field (a);

the "self-energy" of the charge in the context of the molecule's dielectric (b);

and the "screening" interaction of the solvent on charges within the molecule (c).

This, when added to the potential at a charge due to its own field, _i(i), yields the total potential.

(eqn. 11)

Note that while the potential at a charge due to its own Coulomb field is infinite, it is easy to remove analytically (simply not including it in the sum over charges). It appears on the grid as a non-infinite, artifactual, potential. This can be removed by analytic or numerical techniques.

ZAP

What makes ZAP different from previous PBE solvers? Consider the PBE (eqn. 5) rewritten so:

(eqn. 12)

The second term on the LHS (left hand side) is the Laplacian operator. If this were the only LHS term the solution would be Coulomb's Law (eqn. 1). The first term represents the polarization of the solvent and is non-zero only where the dielectric constant is varying.

As is shown in eqn. 13, this can be thought of as a polarization "surface" charge, (r). Some methods of solving the PBE explicitly make use of this reformulation: Boundary Element methods explicitly calculate the polarization charge and then use this to calculate potentials within or exterior to the molecule.

(eqn. 13)

The problems of grid-based methods such as DelPhi arise because the physical description of the dielectric is discontinuous. It is low inside the molecule, high outside and the transition between is infinitely sharp. Not only is this unphysical, it is very hard for grids to represent because the transition is unlikely to fall exactly on a grid point.

ZAP solves this problem by basing the dielectric description upon atomic-centered gaussians. This creates a dielectric function that varies from internal to external values smoothly over a range of a few 1/10th of an Ångstrom. The ZAP solution of the PBE is therefore much more robust and precise. (In addition, because we can easily calculate the derivative of the dielectric, a simple numerical trick allows us to calculate solvent forces.)

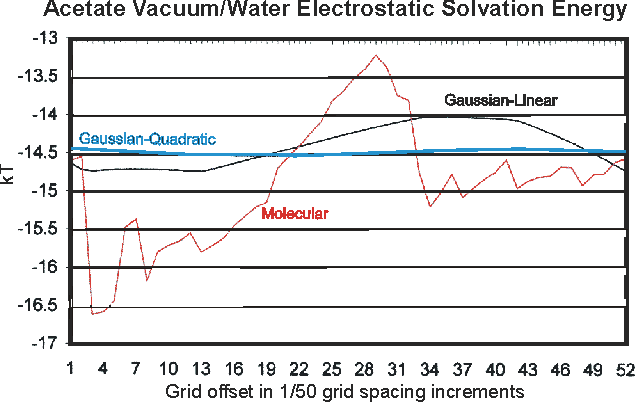
An example of the improved behavior of ZAP over DelPhi is shown in the figure below. Here we have changed the "register", i.e. the precise placement of the molecule on the grid, by successive increments of 0.02 of a grid spacing and plotted the energy due to the solvent reaction field. The DelPhi-like approach (labeled "Molecular" on the graph) leads to a jagged, almost random-walk line. The two ZAP curves represent different ways of mapping the molecular charge on to the grid. The older, DelPhi-like method leads to a curve that still retains some kinks and has substantial variation. When the new ZAP method (quadratic interpolation) is used the variation becomes smooth and almost negligible.

Electrostatic Potential Maps

As a grid-based PBE solver, ZAP naturally produces grid output. The most basic of these is the raw potential map. Each grid point is assigned a potential (in kT/e), i.e. a value of 1.0 means the energy for a unit charge at this point is 1 kT (0.591 kcal/mol). The potentials inside the molecule from this map are not particularly interesting because they are dominated by the atomic charges. Outside the molecule, however, potentials take on the character of the solvent-screened field.

Another map that ZAP can produce is the effective induced charge from the solvent, i.e. the first term in eqn. 12, which represents the net solvent polarization. For PBE models where the dielectric varies discontinuously at the surface, this charge forms an infinitely thin layer around the molecule. In ZAP the surface charge is distributed around the surface in a layer of a few tenths of an Ångstrom.

Quantities that can be calculated from the raw potential map are the atom potentials and the atom-by-atom contributions to the solvation energy. The first have a slight complication: the actual potential at a charge is infinite due to its own Coulomb field, _i(i). This is overcome by analytically removing this self-contribution. The result is the potential at each atom from the solvent and every other atom in the molecule. The second set of quantities is the potential produced by the solvent at each atom multiplied by half the charge on that atom. The sum of this quantity over all atoms is the energy of bringing a molecule from a media of dielectric equal to the molecule (e.g. organic solvent) into water.

Related Electrostatic Properties and Metrics

Other electrostatic and molecular properties may be derived from the ZAP calculation. These include:

Total Molecular Charge
Sum over Absolute Value of Charges
Surface Area (Molecular Surface or Accessible Surface)
Fraction of Surface Area between specified or default ranges
Number of patches of surface greater than or less than specified or default thresholds
Fractional area of largest patch greater than or less than specified or default thresholds
Molecular Volume
Molecular Steric Quadrapole Moments (three)
Contracted Steric Octapole Moments (three)

The first two quantities are straightforward. The net charge is obvious and the sum of the absolute value of each atomic charge is a measure of molecular polarity (e.g. polar molecules will have a larger value than non-polar).

Surface area is a key concept in many molecular descriptors and ZAP provides either the accessible (that formed by expanding the radius of each atom by the radius of water ~ 1.4 Å) or the molecular (that formed by the inner surface of a ball the radius of water rolled over the molecule) area. Each point on a surface can be assigned a potential from the raw ZAP potential map. We can contract this information in several ways. Given certain potential thresholds we can ascertain what fraction of a surface falls between or beyond these limits. For example, limits of -1 and +1 kT would produce three fractions: surface of potential less than -1 kT, surface of potential between -1 and 1 kT, and surface of potential greater than +1 kT. ZAP contains default threshold values that have been designed to produce contributions to each range or "bin" for typical molecules.

Another analysis of surface information is via connectivity. If we remove all parts of the surface that are less than a given potential the resultant surface will consist of "islands" of positive potential. For simplicity ZAP only reports the number of such and the size of the largest as a fraction of the total surface area. We may also wish to set a negative threshold, i.e. remove all surface with potential greater than some value to calculate negative patches. These thresholds may be set by the user or left to default to the maximum and minimum threshold values from the range analysis described above.

Finally, there are volume characteristics. This has relevance to electrostatics as it represents the amount of physical space assigned a low dielectric value. The first such parameter is the molecular volume. The second are a triplet that are analogous the the moments of inertia, and the third are a triplet that measure the degree of deviation from ellipsoidal symmetry.